 | New Millennium Golf Science
where golf myths get debunked
"It's not what you don't know that hurts you, it's what you know that just ain't so." -- Mark Twain |
Repeat after me…
There is no centrifugal force…There is no centrifugal force…There is no centrifugal force
THERE IS NO CENTRIFUGAL FORCE!
Houston we have a problem… How do I explain a mathematical problem without losing an audience that may not be well versed in mathematics? There is no easy way. I'm going to start at the beginning (first principles). All I ask is that you forget about everything you may have heard about non-interial (rotating) coordinate systems (in which the fictitous centrifugal force does play a role). They're not necessary; and in-fact have no place in golf swing mechanics. We have much to cover so lets begin.
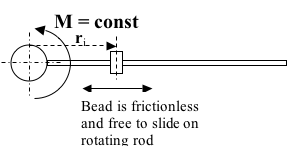
On a discussion board mandrin posed a problem. He asked the reader to imagine a rod with bead on it having no friction (so it can slide easily). The rod spins about a axis through one end and is subject to a constant hub torque: M. Mandrin claims that the bead moves radially outward as the rod accelerates because it is subject to "centrifugal force". That's nonsense and on this page we will prove it using well established Engineering Mechanics. First we will consider the kinematics.
kinematics: the study of motion without considering forces and torques
Kinematics of a Particle subject to:
Plane Curvilinear Motion - in Polar coordinates (r - θ)
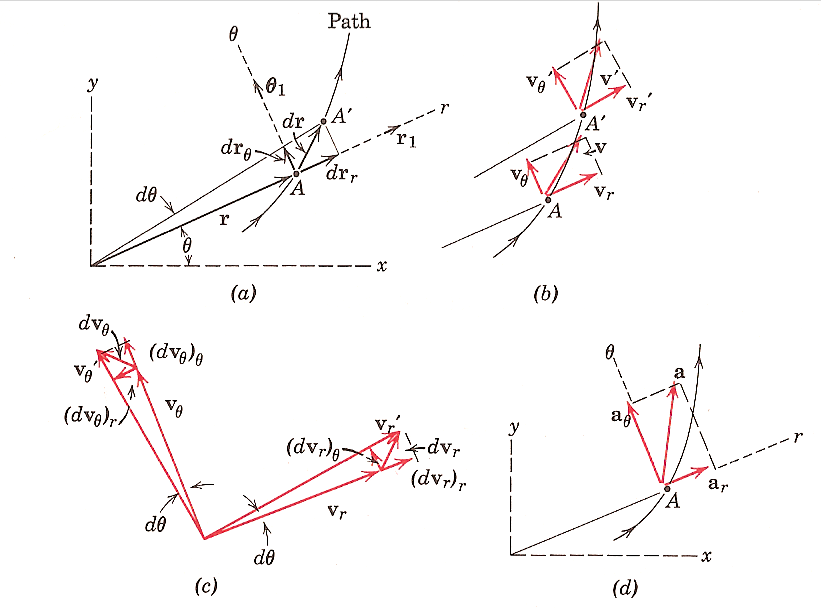 Fig 1
Fig 1
mandrin's problem is best suited to polar coordinates as shown in figure 1. First lets derive the equation for velocity of the particle (remember the particle is a bead which slides freely on a rotating rod) Velocity is a change in location (show by the vector r in fig 1a) with respect to time. In figure 1a, the differential displacement dr of the particle (which again, in our case is the bead sliding along the rotating rod) between location A and A' is represented by two components: dr = drθ + drr There is a radial component: drr which represents the bead sliding away (or towards) the axis of rotation and there is a a drθ component which has a magnitude equal to the length of the equivalent differential arc: r dθ Division by the time increment and taking the limit (calculus) gives the two components of velocity:
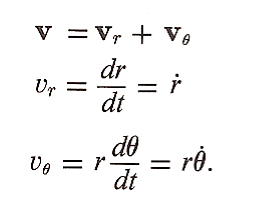
Fig 2
Now that we have the relationship of the two components of velocity of a particle in curvilinear motion given polar coordinates, lets derive the acceleration of the particle. We need to know what constitutes the acceleration of a particle so we can use Newton's equations of motion ( F = ma ) to solve for the path or trajectory of the bead given the (real) external force (due to the hub torque M) acting on it.
Refer now to fig 1b. As the particle (bead) moves from A to A', the two velocity components vr and vθ undergo a vector change as shown in fig 1c. Notice, there are two radial components of acceleration (dvr)θ and (dvr)r and there are two &theta components of acceleration: (dvθ)θ and (dvθ)r. What we have shown graphically, strictly through examination of the kinematics is that the acceleration of a particle subject to curvilinear motion in a plane given a polar coordinate system has four (4) separate elements: two for each direction. Remember this as it is important.

Fig 3
Kinetics of a Particle subject to
Plane Curvilinear Motion - in Polar coordinates (r - θ)
Now that we have derived using kinematics the equation for acceleration we can consider the forces and answer the question that's being asked.
Remeber the question is: Why does the particle (our bead) move relatvive to the rod? What causes it to move out if the only force acting on it is the (tangential) one in the θ direction?
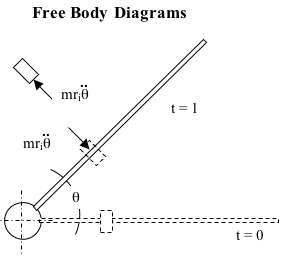
Fig 5
As shown in the free body diagram of figure 5, there is only one external force acting on our bead! (No centrifugal force) The only force acting on the bead is that due to the rod accelerating as a result of the torque M at the hub. Assuming the mass of the bead is negligible in comparison to the mass of the rod, then moment of inertia (I) of the rod is not effected by the location of the bead. Therefore the angular acceleration d2θ/dt2 is constant and has a magnitude of M/I. In other words, the force on the bead (and rod) is a function of the radial distance from the center of rotation and has a direction that is always (only) in the θ direction. Again… there is no force acting on the bead in the radial direction… and yet the bead moves away from the center. Here's why…
What we've done below is substitute the acceleration (a) which we determined strictly from the kinematics in to Newton's equation of motion: F=ma.

Fig 6
Look at the second equation in figure 6. Note that the sum of Forces is zero… zip… nada… stated another way… there are no forces (centrifugal or otherwise) acting on the bead in the radial direction yet that equation is telling us the bead will accelerate in a radial direction: d2r/dt2 = r(dθ/dt)2. The radius r changes as a function of the angular velocity squared ω2=(dθ/dt)2 THAT'S ALL THERE IS TO IT! Simple classical mechanics ... no imaginary; made up; completely wrong "centrifugal forces" are involved. This make perfect sense if you've been following the discussion. The centripetal force requirement was mentioned earlier. In the absence of a centripetal force any mass will deviate from a circular path.
What have we learned? Lets review...
There is no centrifugal force acting on the bead
The kinematics explains why the bead moves radially
There is absolutely no need to resort to patently wrong magical mystical totally nonsensical centrifugal force theories. Classical mechanics and a firm grasp of technical concepts are all that are needed.
|