Lets begin by making some assumptions since we will soon be running some numbers: So then what we have here is a Single degree of freedom system:  Where: K is easily determined from mechanics of materials which tells us: We compute the cross-sectional area A from the typical steel golf shaft weight:
Now we have everything we need to calculate the resonant frequency of our single degree of freedom (SDOF) mechanical system . Every physicist knows the resonant frequency of a SDOF is given by:
 You may wonder why we need to know the natural frequency of our SDOF mechanical system. It has to do with the concept of impedance matching. You can think of the mass-spring SDOF system as a filter which has the ablility to allow forces to pass (in this case to the larger 100,000 kg mass) or to stop them dead in their tracks. If things are such that the impedance matches, then the force of the impact of the ball will be felt by the larger mass on the other side of the shaft "spring" and it will contribute to the "effective mass" of the collision. Impedance matching concerns whether the frequency of the excitation (ball contact force vs. time) is above or below the natural frequency of the mechanical system: If the excitation frequency is below the natural frequency of the system, then the large mass comes into play. If the excitation frequency is above the natural frequency then the large mass is "isolated" by the mass spring SDOF system and the large mass does not come into play. Of course there is a continuum and if per chance the frequencies just so happen to match.... well then we have "resonance" and in that case then that would be like the ball hitting a massive hard surface.
So lets calculate these frequencies… which is 1/2 a cycle orfd = 4651 Hz Therefore fd/fn = 4651 / 484 = 9.6 >> 1.4 ! Ah ha! We now find that the excitation frequency is considerably above the natural frequncy of our club head mass on a shaft (mass spring SDOF) sytem. UNDOUBTEDLY the large mass will be isolated when we consider the "effective" mass Ma in the collision equation given below:
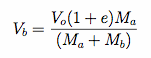
 So then… that is the answer. Even in this extreme case, since Ma will not be significantly higher for the impact in figure 1 of the poser's question, The ball velocity Vo will be almost the same as when it departs in case of figure 2 where Ma is limited to 0.2 kg. You know what is really surprising? That's right … the poser actually got the answer to his own question RIGHT for a change (though he failed prove it and was undoubtely guessing having a 50% possibility of guessing correctly. That is if his goal all along wasn't to kiss bm ass… what a brown-noser)
Maybe you're saying wait just a minute! The force caused by the collision is an impusle not a sinusoid and therefore we're not dealing with simple harmonic motion. This is true so lets consider the time it takes for the shock wave to reach the heavy mass. To do this we need to know the wave speed of in steel. Wave speed is given by the square root of the ratio of the bulk modulus to the density where bulk modulus is a measure of how "compressible" a material is.  So the time it would take for the shock to reach the mass and return to the club head would be: 3 / 4512= .00066 seconds. But Frank Thomas has already told is the ball is gone in 0.00043 seconds. Its gone before the wave even makes it to the large mass and back! Therefore no reflected energy can be added to the restitution phase of the collision. In conclusion, the large mass has no effect what so ever. One final thing to keep in mind… As with most things mandrin of la mancha poses the above scenario has nothing to do with golf. In a real swing with a real club the natural frequency of the cantilever beam shaft will be even much lower… well below the excitation frequency. It is safe to say in a real swing the golfer's mass is always complete isolated from what's happening at the club during impact. What have we learned? Lets review...
 Feliz Navidad | ||||||||
| ||||||||
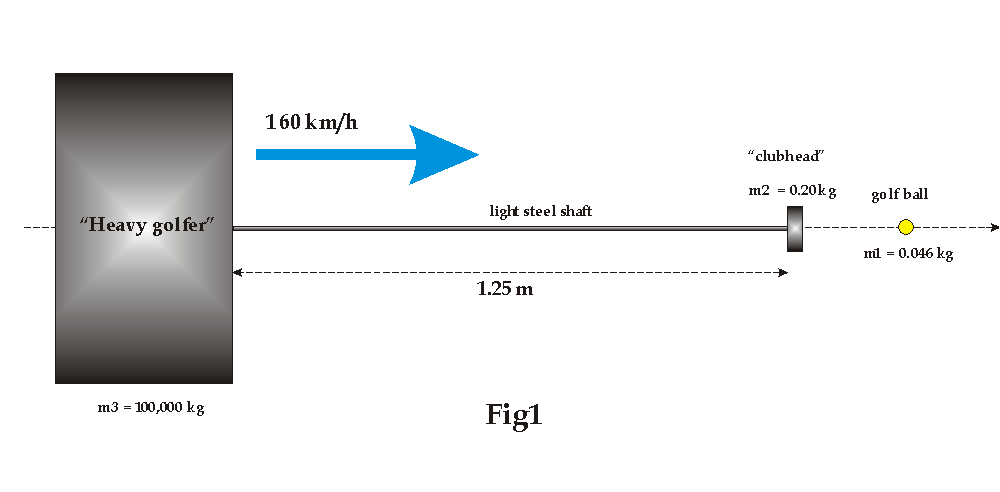
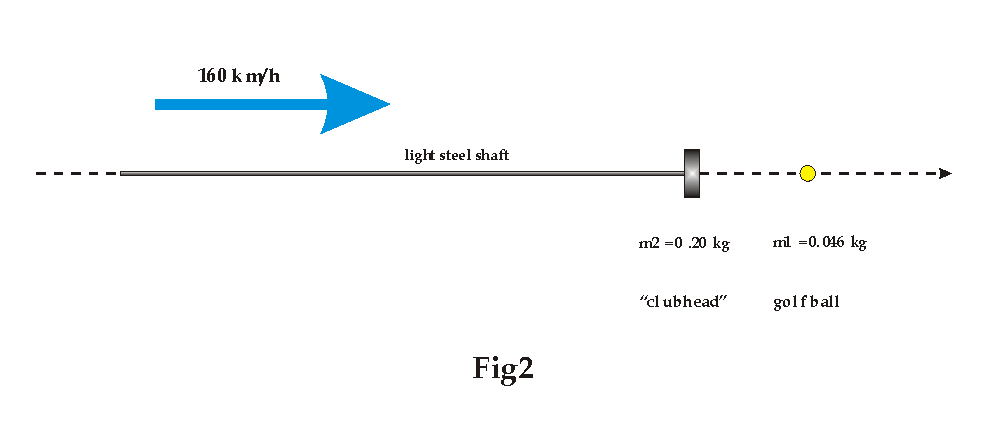To make the situation as extreme as possible the shaft is not aligned sidewise, as occurs when hitting in a real golf swing during impact, but rather length wise. Hence all of the weight of our imaginary 'heavy golfer', weighing only 100000 kg, - equivalent to the weight of 2,174,000 golf balls - is directly bearing onto the ball, at impact.
